-
- Downloads
smaal corrections
Showing
- README.md 1 addition, 1 deletionREADME.md
- dist/libhreels-2.0.1-py3-none-any.whl 0 additions, 0 deletionsdist/libhreels-2.0.1-py3-none-any.whl
- dist/libhreels-2.0.1.tar.gz 0 additions, 0 deletionsdist/libhreels-2.0.1.tar.gz
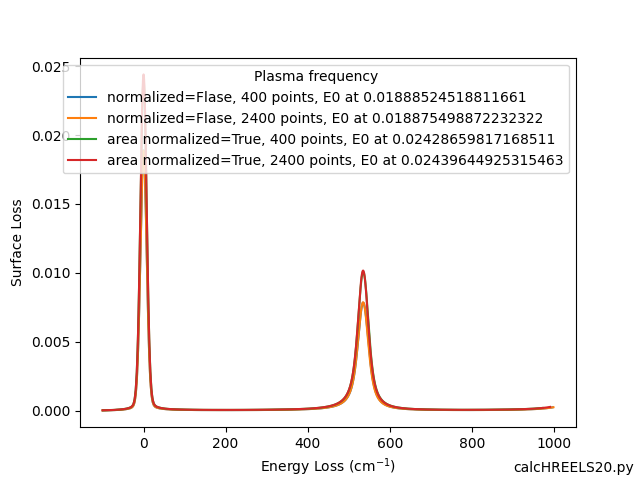
- libhreels/calcHREELS20.png 0 additions, 0 deletionslibhreels/calcHREELS20.png
- libhreels/calcHREELS20.py 6 additions, 42 deletionslibhreels/calcHREELS20.py
- libhreels/dielectrics20.py 19 additions, 23 deletionslibhreels/dielectrics20.py
- pyproject.toml 1 addition, 1 deletionpyproject.toml
dist/libhreels-2.0.1-py3-none-any.whl
0 → 100644
File added
dist/libhreels-2.0.1.tar.gz
0 → 100644
File added
| W: | H:
| W: | H:


